 |
 |
 |
 |
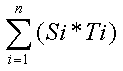 =0
=0  =
=
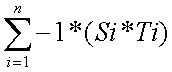 = -1 *
= -1 *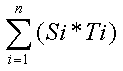 =-1*0=0.
=-1*0=0.| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | Bit poisition |
| C0 | C1 | D1 | C2 | D2 | D3 | D4 | C3 | D5 | D6 | D7 | D8 | codeword pattern |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | Data bits | ||||
| 1 | 1 | ¿ | D1 contributes check bit pattern 11 (bit position 3) | |||||||||
| 1 | 1 | ¿ | D3 contributes check bit pattern 110 (bit position 6) | |||||||||
| 1 | 1 | ¿ | D5 contributes check bit pattern 1001 (bit position 9) | |||||||||
| 1 | 1 | ¿ | D6 contributes check bit pattern 1010 (bit position 10) | |||||||||
| 1 | 1 | 1 | ¿ | D7 contributes check bit pattern 1011 (bit position 11) | ||||||||
| 1 | 1 | ¿ | D8 contributes check bit pattern 1100 (bit position 12) | |||||||||
| 1 | 0 | 0 | 0 | Calculate check bit using even parity bit | ||||||||
| 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | codeword generated |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | Bit position |
| C0 | C1 | D1 | C2 | D2 | D3 | D4 | C3 | D5 | D6 | D7 | D8 | codeword pattern |
| E | 4 | F | receive bit patter in hexadecimal | |||||||||
| 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | receives bit pattern |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | set aside received check bits | ||||
| 1 | 1 | ¿ | D1 contributes check bit pattern 11 (bit position 3) | |||||||||
| 1 | 1 | ¿ | D2 contributes check bit pattern 110 (bit position 6) | |||||||||
| 1 | 1 | ¿ | D5 contributes check bit pattern 1001 (bit position 9) | |||||||||
| 1 | 1 | ¿ | D6 contributes check bit pattern 1010 (bit position 10) | |||||||||
| 1 | 1 | 1 | ¿ | D7 contributes check bit pattern 1011 (bit position 11) | ||||||||
| 1 | 1 | ¿ | D7 contributes check bit pattern 1100 (bit position 12) | |||||||||
| 1 | 0 | 0 | 0 | Calculate check bit using even parity bit | ||||||||
| X | positions sent and rcvd check bit not the same | |||||||||||
| 2 | sum of position weight=2 position 2 is garbled | |||||||||||
| 0 | correct the bit. | |||||||||||
| 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | correct codeword |
| A | 4 | F | original codeword sent in hexadecimal. | |||||||||
| 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | Data bits delivered to upper layer |
| 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 |
2a. All double-bit errors E(x)=xi+xj=xi(1+xj-i),
if G(x) is a primitive with degree of c and the length of codeword is
less than 2c-1. It implies that j-i <=2c-1.
g1(x)
has a degree of 5. To check if g(x) is a primitive polynomial, we need
to check if it is not a divsor of 1+xm for any m<25-1=31.
We use the chkprimitive.pl for this. The result is shown in http://cs.uccs.edu/~cs522/hw/hwF2003/hw5ex4a.txt.
It indicated that this is a primitive polynomial and therefore it can
detect any double bit error up to a codeword length of 31.
m(x)=10011101 g(x)=11
length(m(x))=8 length(g(x))=2
degree(m(x))=7 degree(g(x))=1
m(x)=x^7+x^4+x^3+x^2+1
g(x)=x^1+1
mx=1 0 0 1 1 1 0 1
len=1, indexmx=7
d(x)=1 0 0 1 1 1 0 1 0
dx=100111010
1 0 0 1 1 1 0 1 0
1 1
1 0 0 1 1 1 0 1 0
1 1
--------
1 0
1 1
--------
1 1
1 1
--------
0 1
0 0
--------
1 1
1 1
--------
0 0
0 0
--------
0 1
0 0
--------
1 0
1 1
--------
1
r(x)= 1
q(x)=1 1 1 0 1 0 0 1
codewordPacked=100111011
Ans: c(x)=111001100 g(x)=11
length(c(x))=9 length(g(x))=2
degree(c(x))=8 degree(g(x))=1
c(x)=x^8+x^7+x^6+x^3+x^2
g(x)=x^1+1
d(x)=1 1 1 0 0 1 1 0 0
dx=111001100
1 1 1 0 0 1 1 0 0
1 1
1 1
1 1
--------
0 1
0 0
--------
1 0
1 1
--------
1 0
1 1
--------
1 1
1 1
--------
0 1
0 0
--------
1 0
1 1
--------
1 0
1 1
--------
1
r(x)= 1
q(x)=1 0 1 1 1 0 1 1
crc check detects error!
r(x)<>1; crc check detects error
Ans:
g1(x)=x^5+x^2+1; g2(x)=x+1;
x^5+
x^2+ 1
*
x+ 1
x^5+
x^2+
1
x^6+
x^3+ x
x^6+x^5+
x^3+x^2+x+ 1
Yes, G(x)=g1(x)*g2(x)
Assume we use the data bit pattern 11111111. Note that with
g1(x) we can only cover double bit error up to 31 bits (not 2^6-1).
Use encode.pl 11111111 1101111 we got codeword=1 1 1 1 1 1
1 1 1 0 1 0 0 0
Assume we garble first and last bit. The garbled codedword
is 0 1 1 1 1 1 1 1 1 0 1 0 0 1
Use decode.pl 01111111101001 1101111
c(x)=01111111101001 g(x)=1101111
length(c(x))=14 length(g(x))=7
degree(c(x))=13 degree(g(x))=6
c(x)=+x^12+x^11+x^10+x^9+x^8+x^7+x^6+x^5+x^3+1
g(x)=x^6+x^5+x^3+x^2+x^1+1
d(x)=0 1 1 1 1 1 1 1 1 0 1 0 0 1
dx=01111111101001
0 1 1 1 1 1 1 1 1 0 1 0 0 1
1 1 0 1 1 1 1
0 1 1 1 1 1 1
0 0 0 0 0 0 0
--------
1 1 1 1 1 1 1
1 1 0 1 1 1 1
--------
0 1 0 0 0 0 1
0 0 0 0 0 0 0
--------
1 0 0 0 0 1 0
1 1 0 1 1 1 1
--------
1 0 1 1 0 1 1
1 1 0 1 1 1 1
--------
1 1 0 1 0 0 0
1 1 0 1 1 1 1
--------
0 0 0 1 1 1 0
0 0 0 0 0 0 0
--------
0 0 1 1 1 0 1
0 0 0 0 0 0 0
--------
0 1 1 1 0 1
r(x)= 0 1 1 1 0 1
q(x)=0 1 0 1 1 1 0 0
crc check detects error!
c(x)=00000111101000 g(x)=1101111
length(c(x))=14 length(g(x))=7
degree(c(x))=13 degree(g(x))=6
c(x)=+x^8+x^7+x^6+x^5+x^3
g(x)=x^6+x^5+x^3+x^2+x^1+1
d(x)=0 0 0 0 0 1 1 1 1 0 1 0 0 0
dx=00000111101000
0 0 0 0 0 1 1 1 1 0 1 0 0 0
1 1 0 1 1 1 1
0 0 0 0 0 1 1
0 0 0 0 0 0 0
--------
0 0 0 0 1 1 1
0 0 0 0 0 0 0
--------
0 0 0 1 1 1 1
0 0 0 0 0 0 0
--------
0 0 1 1 1 1 0
0 0 0 0 0 0 0
--------
0 1 1 1 1 0 1
0 0 0 0 0 0 0
--------
1 1 1 1 0 1 0
1 1 0 1 1 1 1
--------
0 1 0 1 0 1 0
0 0 0 0 0 0 0
--------
1 0 1 0 1 0 0
1 1 0 1 1 1 1
--------
1 1 1 0 1 1
r(x)= 1 1 1 0 1 1
q(x)=0 0 0 0 0 1 0 1
crc check detects error!
Therefore the G(x) can detect 5 bit error (odd number bit error).